わり算の教え方
「わり算」を「水道方式」ではどのように教えていくのか、教材や資料を例にあげて紹介していきます。
① わり算はなぜ難しいの?
★「わり算」が難しい理由…
小学3年の4月に習う「わり算」。
「なんか難しいことを習うのかなぁ…」と緊張感を抱く子どもたち。お母さんも「うちの子、わり算でつまずかないかしら?」とちょっと心配になったりしますよね。
わり算に対してはどうしても 難しい計算 という印象を持ってしまいます。ではなぜ「わり算」は難しいのでしょう…。
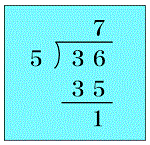
まず思い浮かぶのは、筆算の書き方。
例えば「36÷5」を筆算にすると上のように書きます。
これを子どもたちに読ませてみると、
「5÷36 答え 1 あまり 7」
という子が出てきます。
(正しくは、「36÷5 答え 7 あまり1」)
いままで勉強してきた計算は、すべて左から、あるいは上から読み、一番最後に書いたものが答えだったのですから、わり算になると勝手が違って戸惑ってしまいます。
計算する順番 だって他とは違います。「74÷3」のような場合、まず大きい方の位の「7÷3」から計算します。今までは小さい位からたしたり、ひいたり、かけたりしてきたわけですから全く逆です。
それからわり算の計算は、かけ算、ひき算、たし算 を全て使わなければならない という複雑さがあります。ケタ数が大きくなると大人だってウンザリしますね。途中で何算をしているのかわからなくなる子どもも多いです。たし算・ひき算・かけ算のどれかが不十分な子どもであれば相当シンドイということも想像がつきます。
また、わり算の計算では九九を使いながら近い答えを探すという 試行錯誤 が必要になります。一度立ててみた答えが大きすぎたり小さすぎたりしたら消してやり直すこともありますね。一回で答えが見つかるとは限らずとても面倒です。それに割り切れればスッキリするけれど、やっかいなことに 余りが出る場合もある ので いっそう答えが見つけにくいのです。
余りに関していえば、文章題になると 余りの処理の仕方 も判断が求められるので最後まで気が抜けません。

でも、難しさの最大の理由は、わり算には二つの意味がある ため文章題などで子どもたちが混乱を起こしてしまうことなのです。
これまでも、最初に新しい演算を教えるときは「どんな時に使う計算か」という 演算の意味 を教えることが大事だと書いてきました。では、わり算にはどのような意味があるのでしょうか。
②わり算の意味
★わり算ってどんな時に使うの?
わり算は「分ける」という行動から生まれました。初めてわり算を勉強する子には、「分ける」という作業を体験させて説明するのが良いと思います。
ただ分ければ良いわけではありません。同じに分ける、分けられるところまで分ける、ということが算数の「わり算」にとってたいへん重要です。
わり算 は 同じずつ分けられるところまで分ける計算 です。
そしてわり算の式は
「全体の数÷いくつ分=1あたりの数」 で表します。

最初にジュースなどの液量を分けてみましょう。これだと余りを出さずに最後の1滴まで分けることができます。そしてみんなが同じ量にならなければ不満の声が噴き出します。多い子の分は少ない子の分に移したりしながらピタッと同じになるまで試行錯誤が続きます。
同じに分けるという場面は子どもたちが生活の中でしょっちゅう体験しているので、「わりざん」を身近に感じてくれるかもしれません。
このようなとき、1人分の数を求めるのが、「わり算」 というわけです。
では、具体的に分ける場面を設定して、わり算を教えてみましょう。
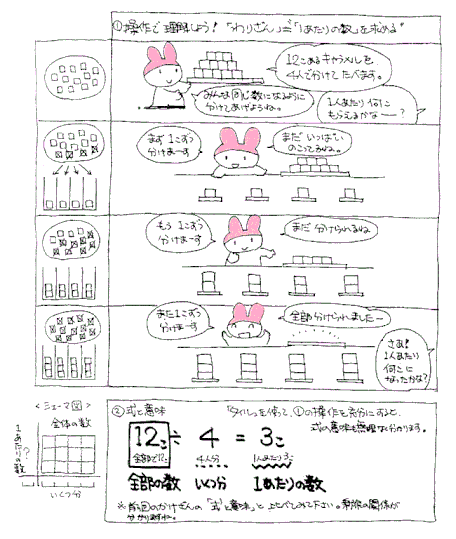
キャラメルが12個あります。子どもは4人います。ケンカにならないように同じ数ずつ分けます。1つずつ配っていくと1人あたり3こもらえます。これが 「1あたりの数」を求めるわり算 です。
もしお家でお子さんにわり算を教えるならチョコやキャラメルなどを使って同じずつ分けられるところまで分けてみてはいかがでしょう。「1人何個かな?」という時、自分の目の前にキャラメルが3個くると「わり算の答えってこれか!」と実感でわかりますよね。学校ではお菓子を使うことはできないけど、家庭でならこんな算数体験が良いかもしれません。
12個のキャラメルを4人で分けるとき、1個ずつ配っていくという操作をします。
今度はタイルでも配るという操作をして、これを「わり算の式」に表すようにします。
★わり算の意味の二つ目って?
わり算とは、同じずつ分けられるところまで分けて「1あたりの数」を求める計算でしたね。実はわり算にはもう一つの意味があります。
わり算は「いくつ分」を求める計算でもあります。全体の数と1あたりの数も分かっているとき、いくつ分を求めるためにはわり算をします。
そして、「いくつ分」を求めるわり算の式は
「全体の数÷1あたりの数=いくつ分」 という式で表します。
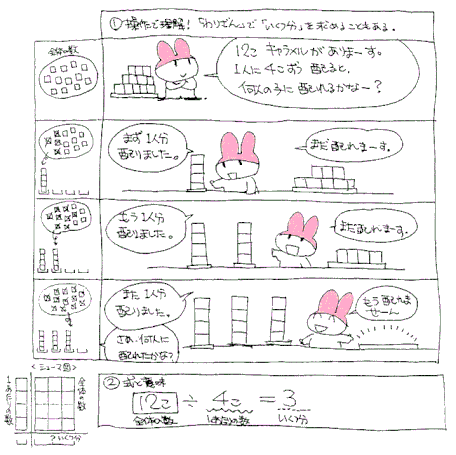
12このキャラメルを一人に4こずつあげます。何人の子にあげられますか?
3人ですね。
わり算は二つの意味があるので子どもたちにとって難しいのです。
算数の教科書では「1あたりの数」を求めるわり算が出てきてすぐに「いくつ分」を求めるわり算が出てきます。なので子どもたちも整理がつかないまま、問題がごちゃ混ぜに出てきてわからなくなる…というわけです。
水道方式の指導では、「1あたりの数を求めるわり算」をわり算の基本と考え、先に学習します。そしてわり算の意味がしっかり定着し、計算の手順に慣れてきた後で、「いくつ分を求めるわり算」を指導しています。ちなみに、数学で育ちあう会のわり算教材では、4ケタ÷1ケタの計算を学習した後で指導しています。
では、わり算の二つの意味を整理しておきましょう。(数学で育ちあう会 F教材より)
③わり算の筆算 〈その1〉
★『筆算』を早い段階で取り入れます
現在の小学校算数では、わり算のタテ書きの計算=「筆算」 が出てくるのは4年生です。「72÷3」のように答えが2ケタになる計算でようやく筆算を取り入れています。
3年生の教科書では商(わり算の答)が2ケタになる「40÷4=10」のようなものや、余りの出るわり算、例えば「19÷4=4あまり3」なども出てきます。でも筆算を教えないため横書きの式で計算させています。余りを出す場合は頭の中で「19-16」のひき算をすることになり、ちょっと大変です。
私たちは1ケタで割る段階から筆算を取り入れるべきだと考えます。筆算ならケタ数がどんなに増えても同じ計算の手順でできる からです。
わり算の筆算は、予想をつけて商を たてる → かける → ひく という手順で行います。

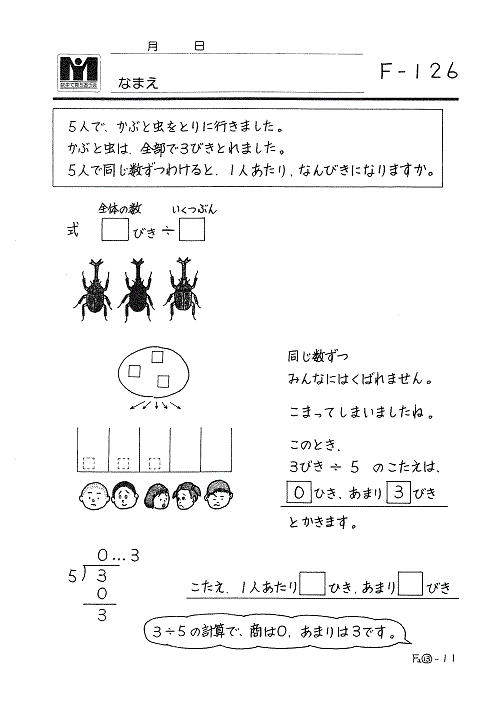
ところで、教科書が扱っていない基礎的なわり算があります。「3÷5=0あまり3」のような商が0で余りが出るわり算は単独では全く出てきません。これらは必要ないと考えられているようです。
けれど、後に出てくる「53÷5」や「535÷5」などの筆算では「3÷5=0あまり3」の計算が必要になってきます。子どもたちは戸惑ってしまい、次のような間違いがよく見受けられます。

私たちは「3÷5=0あまり3」もわり算の基礎の一つと考え、次のような例題で指導しています。
★商(わり算の答)が2ケタになるわり算もタイル配りで納得!
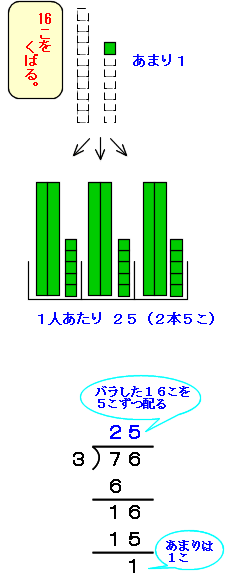
商が2ケタになるわり算、例えば「76÷3」などは、タイルを配ることで計算の順序を説明するとよくわかります。
〈もんだい〉
76枚の折り紙を3人で分けます。一人あたり何枚になりますか?
また何枚あまりますか?
この問題はわり算で求めるので、
式は
76÷3 になります。
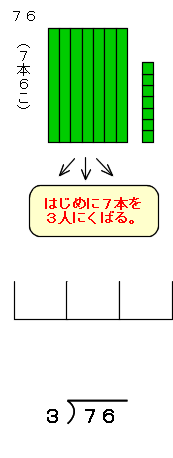
「76」をタイルで置きかえると、「7本6こ」 となります。では、7本と6こを3人で分けてみましょう。
※1個のタイル□が10個集まると「1本」のタイルになります。タイルの数の仕組みについては【かずの教え方】の「十進記数法」とタイルをどうぞ。
このとき、もし7本をバラタイルにくずしてから76このタイルを3人に配り出すと大変手間がかかります。先に7本のタイルを配ったほうがずっと楽ですね。「わり算は大きい方の位から計算する」理由 がここにあります。たし算、ひき算、かけ算はみんな一の位から順に計算してきましたが、わり算だけは逆からのほうが合理的なわけです。
↓↓↓↓↓↓↓↓↓↓↓↓↓↓
7本を3人に配るので、「7本÷3」を計算します。
このとき、3人に2本ずつ配れて、1本あまりますね。
これを筆算の計算と結びつけて考えます。
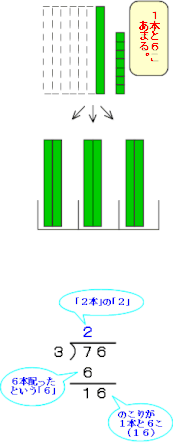
7本は3人で分けると2本ずつ配れるので、商に2をたてます。 たてる
3人に2本ずつ配ったので、3×2本=6本 …かける
7本から6本をひくので、7本-6本=1本 …ひく
バラタイル6こをおろします。おろす
のこったタイルは1本6こ ですね。
↓↓↓↓↓↓↓↓↓↓↓↓↓↓
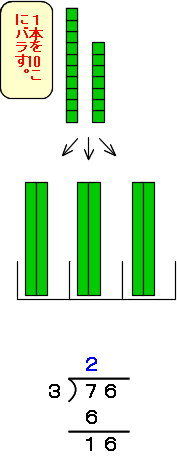
このままでは1本のタイルが配れないので、10このバラタイルにくずします。
↓↓↓↓↓↓↓↓↓↓↓↓↓↓
つぎは、のこりの16こを3人に配るので、「16こ÷3」を計算します。このとき、3人に5こずつ配れて、1こあまりますね。これを筆算と結びつけて考えます。
16こは3人で分けると5こずつ配れるので、
商に5をたてます。 たてる
3人に5こずつ配ったので、3×5こ=15こ …かける
16こから15こをひくので、16こ-15こ=1こ …ひく
これ以上は分けられないので終了。
76÷3=25 あまり 1
こたえ 1人25枚 あまり1枚
こんなふうに、わり算の筆算は
★上の位から順に計算する
★〈たてる〉→〈かける〉→〈ひく〉→〈おろす〉の4拍子をくり返す
ということがタイル配りを通してよくわかります。
わられる数がどんなに大きくなっても4拍子の手順をくり返せば良いわけです。
④ わり算の筆算 〈その2〉
★わり算の筆算攻略法!
さて、前回はわり算の筆算をタイル配りに合わせて説明しました。
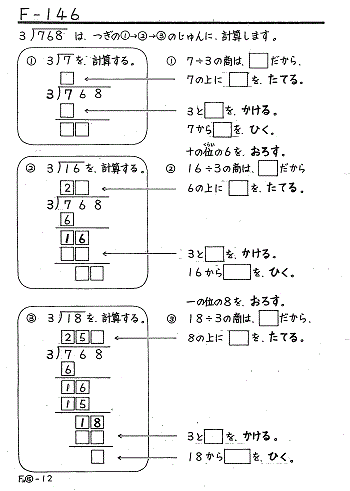
ここで、筆算の手順をまとめます。
大きい方の位から、
たてる→かける→ひく→おろす の順に
分けられなくなるまでくり返します。
この「たてる→かける→ひく→おろす」の4拍子の手続きは子どもが覚えやすく、わる数のケタが増えても通用します。
4年生のわり算では、「÷2ケタ」が出てきて一段と難しくなります。
ケタ数が増えて難しいのは、商(わり算の答)の立つ位置がどこかがわからなくなること。そして、どれくらいの商を立てたら良いのかが見つけにくくなることです。
実はここでつまずく子どもが大勢います。問題の型分けをしてていねいにステップを踏んでいかないとわり算が苦手になってしまいます。でもきちんと系統的に学習すれば、わり算の計算の心地よさが好きになり算数に自信がつく子も多いのです。また、わり算がしっかり習熟できていると、小数のかけ算、わり算もそれほど難しくはないでしょう。
では、「水道方式」ではどのような方法でわり算の筆算を教えているかを一部、ご紹介しましょう。
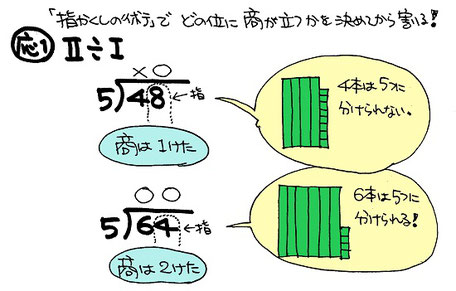
商の立つ位置を決めるには、「指かくしの術」 を使います。
わられる数の最も大きい位に注目させるため、右側の位を指で隠しておきます。そして分けられるならば○、分けられなければ×をし、さらに右隣の位まで指をずらしていきます。こうして始めに商が何ケタになるかを決定します。
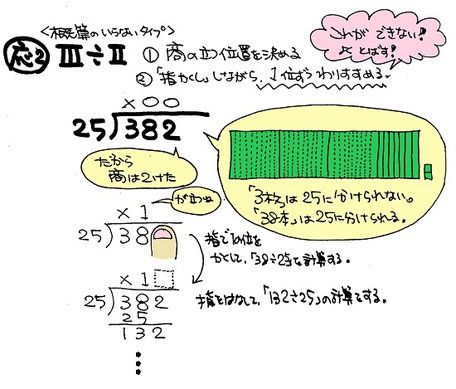
÷2ケタも同じです。商の立つ位置を 「指かくしの術」で決定します。
ここでもタイル配りで考えてみましょう。3枚のタイルは25に分けられないから「38本」に直して分けることになります。
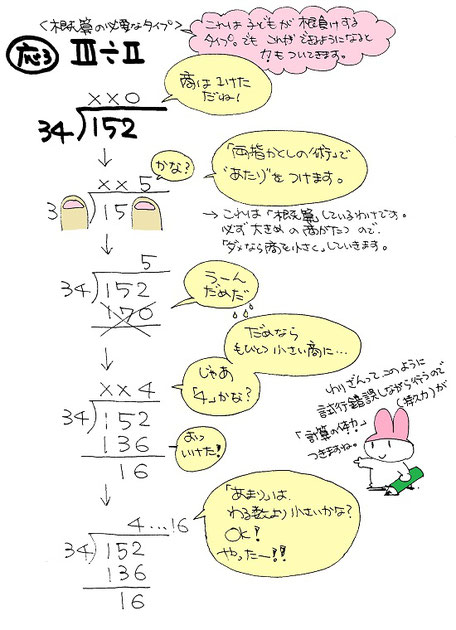
今度は、どのくらいの商を立てたら良いか、見当をつけるための方法です。
これには 「両指かくしの術」 を使います。
だいたいの見当は立ちます(仮商)が、「かける→ひく」をやってみないと本当の商かどうかがわかりません。もし大きすぎたら1つずつ商を減らして同じように確かめていきます。
注意しないといけないのは、「あまり」がわる数より小さいかどうかです。それを確かめてOKなら商を決定できます。
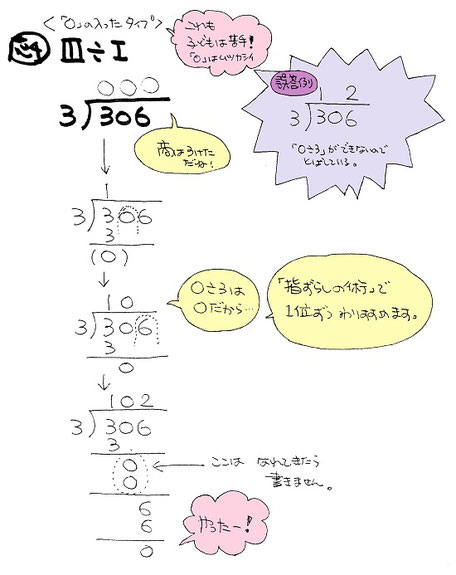
「0」の入ったタイプは間違いが最も多い型です。混乱するお子さんは、0の計算のところも省略せずに一つ一つ書いていくことをおすすめします。

このタイプは、教科書の欠陥がもろに影響して、子ども達が戸惑う型です。大事な要素を抜かさず教えることの大切さをつくづく感じます。
⑤ふたたび、わり算の意味
★わり算の二つの意味、「等分除」と「包含除」
わり算には二つの意味があることは前に説明しました。
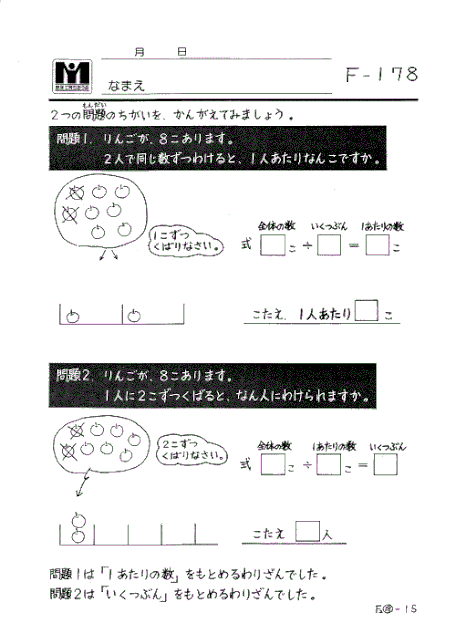
一つは、「全体の数÷いくつ分=1あたりの数」 で、これを難しい言葉で「等分除」(とうぶんじょ)と言います。
もう一つは、「全体の数÷1あたりの数=いくつ分」 で、こちらは「包含除」(ほうがんじょ)と言います。
同じわり算でも求める答が違います。この違いはタイルで考えると次のようになりました。

「水道方式」では、「1あたりの数を求めるわり算=等分除」をわり算の基本と考え、筆算の方法を学習し終わるまでは(数育会では4ケタ÷1ケタまでは)、「等分除」で一貫させています。そして計算の手順がしっかり身についた後で初めて、もう一つのわり算、「いくつ分を求めるわり算=包含除」 を指導しています。
一方、3年生の教科書では、先に「等分除」で導入はしますがすぐ後に「包含除」を出してきて、それ以降はこの二つを(教える側の都合に合わせて)ごちゃ混ぜに登場させている場合が多いのです。
私たちがわり算の筆算を「等分除」で通して教えるのには理由があります。一つにはこれまで見てきたように、筆算の計算法が「等分除」の意味に基づいて行われる からなのです。
例えば「76÷3」を計算する場合、タイル「7本と6個」にし、最初に大きい位の7本から分けるほうが合理的だと述べました。(詳しくはこちら) 同じに分けて1人分の数を求めるのでこれは「等分除」になりますね。もしこれを「包含除」にするとどうでしょう。「76個」のバラタイルを3個ずつまとめていくことになり、「上の位から計算する」必然性が無くなってしまいます。
わり算の計算の手順も日常的な「分ける」という操作と結びついています。だから、いま何を学んでいるか が一番よく分かる方法で指導をするわけです。わり算の筆算を習得すれば、後に習う「包含除」は全く同じ手順で計算することができます。
【例えば「6÷2」を教えるとき】
「6の中に2がいくつ(分)入っているか」とか
「6から2は何回引けるか(累減)」という教え方があります。これらは「包含除」的教え方だと言えます。
「等分除」も「包含除」も重要なわり算です。けれども2つの重要な概念を同時に教えると子ども達は混乱します。文章題で「何算にするのかわからない」というつまずきもこのことが大きな要因と考えられます。なので私たちは「等分除」で1つの概念を身につけてから、次の概念である「包含除」を教えています。2つのわり算を明確に区別し、ちがいを意識して教えるわけです。
後に出てくる、「面積÷長さ=長さ」や、物質密度(g/cm3)・人口密度(人/km2)・速さ(m/秒)の「単位あたり量」などなど、わり算の世界は次々と拡がっていきます。
子どもたちの成長に応じて、わり算の世界が一つずつ確実に心の中に拡がっていくように指導したいと思います。
★わり算とかけ算
「わり算はかけ算の逆でしょ」という教え方を耳にすることがあります。
確かにわり算はかけ算の逆算なのですが、初めて学習する子ども達には、「わり算」が物を分けるという操作から導き出された新しい意味を持つ演算として導入するほうが身近で分かりやすく後への発展性があります。水道方式では、たし算・ひき算・かけ算・わり算を独立してそれぞれ現実世界の量と操作から導入します。そうして後に、「たし算とひき算」、「わり算とかけ算」で互いに密接な関係があることを教えていくようにしています。
さて、わり算は、「全体の数÷いくつ分=1あたりの数」 と、「全体の数÷1あたりの数=いくつ分」 の2つがあると説明しましたが、これを見ると、わり算はかけ算と深い関わりを持つ演算だということがよくわかります。
かけ算 とは、
1あたりの数 と いくつ分 がわかっていて 全体の数 を出す計算です。
「1あたりの数 × いくつ分 = 全体の数」 という式で表します。
タイルの図は次のようになります。
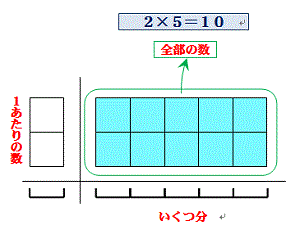
タイル図を見てわかるように、「1あたりの数」と「いくつ分」と「全体の数」の三つの関係から、どれを求めるかによって、かけ算を使うのか、わり算を使うのか、が決まってきます。
このようなタイル図を発展させたものを「かけわり図」と呼んでいます。文章題を解くときにタイル図や「かけわり図」がイメージできれば式が立てやすくなります。
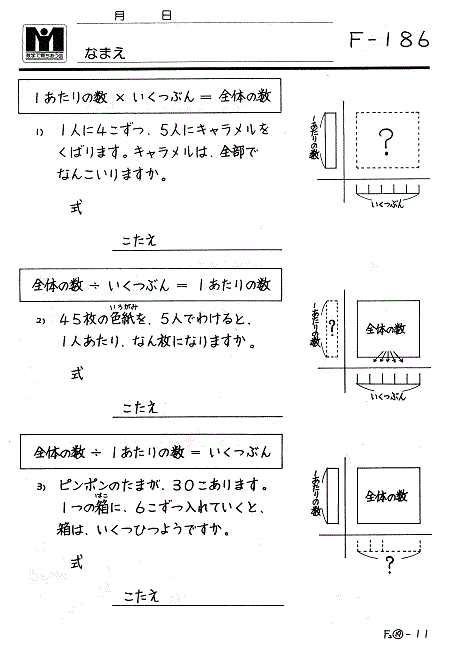
かけわり図」では、1あたりの数が増えれば上に拡がり、いくつ分が増えれば横に拡がり、それに伴って全体の数が拡がります。また液量や重さなどの連続した量にも、そして小数や分数にも使えるので、一貫性・発展性があります。
わり算が「1あたり」を求める演算であることをしっかり理解できていれば、小数・分数のわり算や単位量・割合の理解につながります。わり算とかけ算がわかれば、量の世界が拡がります。小学校算数の基礎・基本を確実なものにして中学・高校の数学へと発展させていくためにも、ていねいにじっくり学習を進めていきたいものです。
